OBJECTIF
Le programme se place dans le cadre de fonctions à valeurs réelles définies sur un intervalle ou une réunion d’intervalles de R.

La diversité des programmes du lycée doit particulièrement inciter à veiller aux connaissances sur les primitives et les intégrales acquises antérieurement ou non par les étudiants. L’accent est mis sur la diversité des approches numérique, graphique et algorithmique, lesquelles contribuent à l’appropriation du concept d’intégrale.

Réf : BOEN Septembre 2013 pages 114/186 et 115/186

Primitives
Primitives de fonctions de référence,opérations algébriques.
Complément : primitives de :
t  → cos(ωt + ?)
t  → sin (ωt + ?),
ω et ? étant réels.

CAPACITÉS ATTENDUES
Déterminer des primitives d’une fonction :
→  à la main dans les cas simples ;
→  à l’aide d’un logiciel de calcul formel dans tous les cas.

Déterminer les primitives d’une fonction de la forme :
→ u'uⁿ (n entier relatif, différent de – 1),
→ u'/u
→ u'e^u

COMMENTAIRES
Pour les primitives de u'/u, on se limite au cas où u est strictement positive.

Intégration
Calcul intégral
Intégrale de a à b de f (x) dx = F(b) – F(a)
où F est une primitive de f .
Propriétés de l’intégrale : relation de Chasles, linéarité et positivité.

CAPACITÉS ATTENDUES
Déterminer des primitives d’une fonction :
→  à la main dans les cas simples ;
→  à l’aide d’un logiciel de calcul formel dans tous les cas.

Déterminer l’aire du domaine défini par :
{M(x, y), a ≤ x ≤ b et f(x) ≤ y ≤ g(x)} où  f et g sont deux fonctions telles que pour tout réel x de [a, b], f(x) ≤ g(x).

COMMENTAIRES
On étudie le cas où  f (resp. g) est la fonction nulle.

On familiarise les étudiants avec quelques exemples de mise en œuvre d’algorithmes liés à des méthodes élémentaires d’approximation d’une intégrale (point-milieu, trapèzes, Monte-Carlo).

Pour les primitives de u'/u, on se limite au cas où u est strictement positive.

Intégration
Calcul d’aires

CAPACITÉS ATTENDUES
Déterminer l’aire du domaine défini par :
{M(x, y), a ≤ x ≤ b et f(x) ≤ y ≤ g(x)} où  f et g sont deux fonctions telles que pour tout réel x de [a, b], f(x) ≤ g(x).

Intégration
Valeur moyenne d’une fonction sur un intervalle :
définition, interprétation géométrique.

CAPACITÉS ATTENDUES
Déterminer et interpréter la valeur moyenne d’une fonction sur un intervalle.

COMMENTAIRES
Cette notion est illustrée par des exemples issus des disciplines professionnelles.

Intégration
Formule d’intégration par parties.

CAPACITÉS ATTENDUES
Calculer une intégrale par intégration par parties.

COMMENTAIRES
Valeur moyenne, valeur efficace dans un transfert énergétique ; centre d’inertie, moment d’inertie.

Primitive: Reconnaître la courbe d'une primitive
Intégrale d'une fonction : résumé du cours Calul Des Primitives et des Integrales (GEOGEBRA)

Décomposition en éléments simples (1)écomposition en éléments simples (2)
Décomposition en éléments simples (3)

Méthode d'intégration : Intégration par parties 
Exercice d'intégrations par parties?
 calculer l'intégrale de 1/(1+2x)

Intégration par partie (IPP)

A maîtriser
pour les chapitres "Séries de Fourier" et "Lois de probabilités"
→  Fiche "Aide mémoire" et exercices

→ Calcul intégral : Approximation méthode des rectangles (17.78 Ko)

Modéliser une fonction par intervalles
Exemple: fonctions linéaires et affines
y = f(x) = ax et y = f(x) = ax+b 

♦ Logiciel de géométrie dynamique / Geogebra en ligne : { https://www.geogebra.org/classic?lang=fr }
♦ Télécharger Applications GeoGebra : { https://www.geogebra.org/download?lang=fr }

♦ Fonction de modélisation par intervalle

→ Lire ou télécharger  la documentation
à télécharger ici
→ DOC : Modélisation d'une Fonction triangulaire par intervalles (142.82 Ko)]
 Le signal triangulaire périodique ci-dessous est constitué
de portions rectilignes (fonctions affines définies par intervalles).

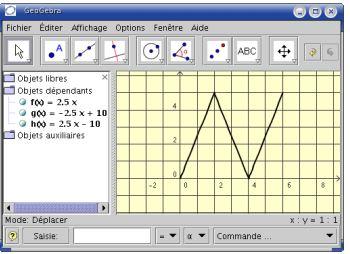
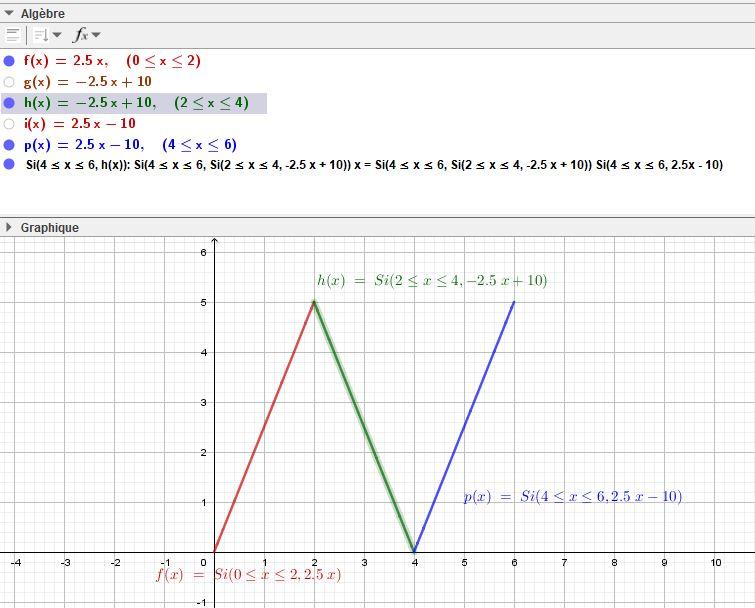
Les deux premiers segments forment le motif périodique, la période de ce signal vaut 4.
Le premier segment est la représentation de la fonction f définie sur [0 ; 2] par : f(x)=2,5x
Le deuxième segment est la représentation de la fonction g définie sur [2 ; 4] par: g(x) = -2,5x + 10
Le troisième segment est la représentation de la fonction h définie sur [4 ; 6] par : h(x) = 2,5x - 10
Dans la zone de saisie (située en bas), on saisit fonction[2.5x,0,2]
[Télécharger ici → DOC : Modélisation d'une Fonction triangulaire par intervalles (142.82 Ko)]

→  Représenter graphiquement
ces équations avec GEOGEBRA

AIDE :
Déterminer et représenter une équation de droite (Fonction affine)

Illustration du cours : Détermination de Fonctions linéaires et affines
Cliquez ici  → Trouver l'équation d'une droite et son coefficient directeur

Des questions ?

→ Comment trouver l'équation d'une droite avec deux points ?
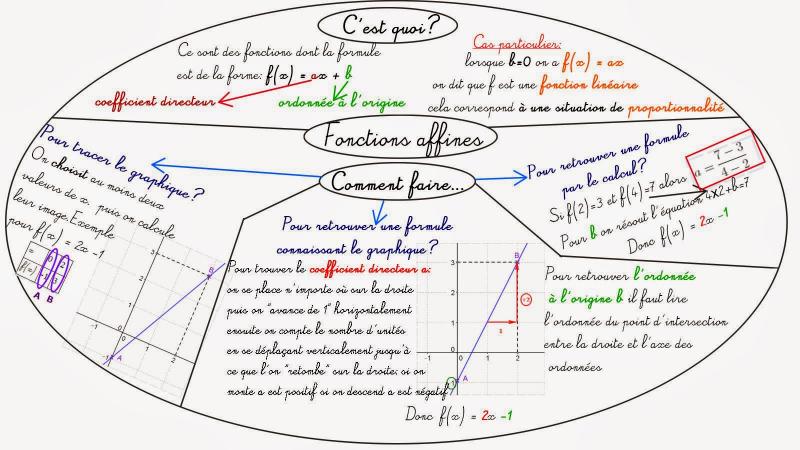
Soient a et b deux réels. L'ensemble des points M(x; y) tels que y = ax + b forme une droite. Celle-ci est la représentation graphique de la fonction affine f qui à x associe ax+b, on dit que c'est la droite d'équation y = ax + b.

→ Comment déterminer l'équation d'une droite linéaire ?
La représentation graphique d'une fonction linéaire est une droite passant par l'origine du repère. On dit que l'équation de la droite est : y = ax. a est aussi appelé le coefficient directeur de cette droite.

→ Comment trouver l'équation d'une courbe à partir d'un graphique ?
Trouver une équation de droite à partir du graphique
• Lecture du coefficient directeur : Lorsque x augmente de 1, y augmente de 2. donc le coefficient directeur de D est 2 : a = 2.
• Lecture de l'ordonnée à l'origine : La droite D coupe l'axe des ordonnées au. point d'ordonnée 1.
• Conclusion : On a donc : f(x) = 2x+ 1.

→ Comment trouver la pente avec 2 points ?
Pour trouver la pente d'une droite, récupérez les coordonnées de deux des points de cette droite, ceux que vous voulez. La pente s'obtient en soustrayant les deux ordonnées de ces points (Y2 moins Y1), puis leurs deux abscisses dans le même ordre (X2 moins X1), et enfin en divisant le premier résultat par le second.

AIDE : DOCUMENTATION GEOGEBRA
Modélisation 3D  → Geogebra 3D (3.74 Mo)

Menu "GEOGEBRA" de la fenêtre graphique
→ Documentation geogebra v5 (3.61 Mo)

MODELISATION AVEC GEOGEBRA

→ Integrale : Approximation Aire par la méthode des rectangles
→ Etude d'une Tension électrique périodique
→ Fonction Triangle
→ Signal triangulaire d'une seule période avec paramétrage par curseur de la fréquence et l'amplitude

METADONNEES DE L'ACTIVITE

Ressource pédagogique initiale originale :
Dans le cadre de la réforme du BTS, activité proposée en 2014 par groupe de travail d'enseignants de BAC STI, BTS et d'inspecteurs :
→ Ressource étude d' une tension - Original (239.89 Ko)

Ressource finalisée et adaptée pour intervention au CFA BTP ALLIER en BTS 1 ère année Electrotechnique pour élèves en statut "Apprenti" :
AUTEURS:
M. Christian Louis MATHIEU pour adaptation avec réalisation d'une proposition de correction en langage LaTeX et usage des TICE :
→ Calcul à la main : détermination d'équations de droites (Résolution système d'équations) , détermination de la valeur moyenne et de la valeur efficace par le calul iintégral.
→ Usage de la calculatrice (TI, CASIO et NUMWORKS) : aide à l'usage avec 3 vidéo collaboratives de M. Elias BERRABAH (Professeur agrégé en poste au Lycée général de  Châteauroux et collaborateur à GEOPROF.FR Clermont)
→ Usage du calcul formel : calcul des primitives et intégrales à partir des formules des valeurs moyenne et efficace (GEOGEBRA: Fenêtre "Calul formel" / Menu icône "F(x)"
→ Usage du logiciel de géométrie dynamique (GEOGEBRA V 5) : modélisation et application dsformules via le champ saisie

Objectif principal :
Application du "Calcul Intégral" à l'électricité pour public "Apprentis"  en BTS Electrotechnique (et par extension tout apprenant de filière Génie Electrique)

Objectifs intermédiaires :
- Modéliser une tension périodique (cas pariculier: signal triangulaire périodique de période T = 2 ms et Umax = 10 V)
- Déterminer la valeur moyenne et la valeur efficace par plusieurs méthodes :  graphique, numériques et calculatoire ; usage des calculatrices courantes (TI 82 ou 83; Casio 25, 35 ou 85 ; Numworks) , utilisation d'appplications numériques de calcul formel et d'un logiciel de géométrie dynamique.
- Effectuer un bilan pour validation et reproductibilité sur autre signal électrique et en vue de la Certification QUALIOPI (Objectifs, compétences, capacités et connaissances, supports pédagogiques).
- Reproduire et valider la séance pour apprentis de la spécialité Fluide Energie Domotique (FED)

Lieu et conditions d'intervention : 
- Salle informatique à 11 ordinateurs pour 11 apprenants de BTS 1ELE
- Séance d'observation organisée par le Directeur pédagogique en présence du Directeur d'Etablissement le  Mercredi 24 mars 2021 de 15h15 à 16h50

FICHE DE SEANCE :
→ Fiche de seance (PDF - 161.17 Ko)

DOCUMENT ELEVE
→  Ressource étude d'une tension périodique - Apprenti (PDF - 1.06 Mo)

PROPOSITION DE CORRECTION
→ Document Elève : Etude d'une tension périodique - Correction-SSI (1.27 Mo)

PRÉ-REQUIS NÉCESSAIRES

• Fonctions linéaires et affines (Niveau collège).
• Fonctions périodiques (Niveau BAC Pro).
• Calcul intégral et propriétés de l'intégrale (Niveau Bac : Primitives et Niveau BTS : Calcul intégral).
• Connaissances de base d'un logiciel de calcul formel et d'un logiciel de géométrie dynamique (Niveau Bac Pro).

Complément sur les aspects énergétiques :
Connaissances en lien avec la physique appliquée (Electricité et sources d'énergie) :  
Télécharger ici  → Rappel de cours "Les sources d énergie" (1.1 Mo) // Auteur : Lycée P. Mendès France Epinal

OBJECTIFS DE L'ACTIVITÉ

• Approche numérique et graphique d'une valeur moyenne d'une fonction sur un intervalle.
• Utilisation d'un logiciel de calcul formel et d'un logiciel de géométrie dynamique.
• Utilisation de la calculatrice pour vérifier les résultats en appliquant la relation de Chasles.

SUJET D'ETUDE
Calcul intégral
ÉTUDE D'UNE TENSION PÉRIODIQUE

DOCUMENT ELEVE
→  Ressource étude d'une tension périodique - Apprenti (PDF - 1.06 Mo)

On appelle u ( t ) la tension en volts en fonction du temps t ( en ms ).
Étudions la valeur moyenne < u( t)) > et la valeur efficace U de cette tension u ( t) sur une période.

La valeur efficace d'une tension périodique est la tension continue constante qui dissiperait la même puissance qu'un dipôle purement résistif.
En Physique, on mesure la valeur moyenne <(u (t )> à l'aide d'un voltmètre en position DC, et la valeur efficace U à l'aide d'un voltmètre en position DC+AC.

Valeur moyenne < u (t) >  de u(t)
Valeur efficace U de u(t)

utilisation du calcul formel sous geogebra  ou sous Photomath avec le calcul de primitives F(x)

à insérer ...

Valeur moyenne < u (t) > de u(t)
Valeur efficace U de u(t)

utilisation du calcul formel
sous geogebra  ou sous Photomath
avec le calcul de primitives F(x)

à insérer ...

MODELISER UN SIGNAL PERIODIQUE TRIANGULAIRE SUR UNE PERIODE
U : Amplitude du signal et T : Période du signal

GEOGEBRA V5 / Entrez dans la zone de saisie :
   Si[x > 0 ∧ x < T / 2, 2 U x / T, Si[x > T / 2 ∧ x < T, 2 U (1 - x / T), 0]]

   

→ 2 curseurs sont créés, respectivement :
U : Valeur maximale du signal (ou amplitude) et T : Période du signal
→ la fonction dans la fenêtre algèbre s'affiche :
     f(x) = Si(x > 0 ∧ x < 2 / 2, 2 * 13.3 x / 2, Si(x > 2 / 2 ∧ x < 2, 2 * 13.3 (1 - x / 2), 0))

Télécharger  ici → Fonction Triangle Période T Amplitude U  (12.37 Ko)

MODELISER UN SIGNAL PERIODIQUE TRIANGULAIRE INFINI
U : Amplitude du signal et T : Période du signal

GEOGEBRA V5 / Entrez dans la zone de saisie :
y=A asin(sin(P x))

→ 2 curseurs sont créés, respectivement
A : Amplitude et P : Période

 Source et fonctions vérifiées et testées le 06 mars 2021 {CLM}
https://help.geogebra.org/topic/signal-triangulaire

MODELISER UN SIGNAL PERIODIQUE RECTANGULAIRE INFINI
a : Amplitude du signal et T : Période du signal
GEOGEBRA V5 / Entrez dans la zone de saisie :
f(x)=2 a (floor(x/T) - round(x/T) + 0.5)


→ 2 curseurs sont créés, respectivement
a : Amplitude du signal et T : Période du signal